財務関数
数値 CTERM (〈利率〉,〈満期目標額〉,〈元金〉)
機能
複利計算で〈元金〉が〈満期目標額〉に達するまでに必要な期間を求めます。
〈利率〉は月利とし、年利を使うときは12ヶ月で割ります。
CTERMは以下の式を用いて求めます。
LN(〈満期目標額〉/〈元金〉)/LN(1+〈利率〉)
※ LN は自然対数
例
1,000,000円を年利8.7%で運用したとき、2,000,000円になるまでの期間を求めます。
CTERM(8.7%/12,2000000,1000000) → 95.952664ヶ月(約8年)
数値 DAMT (〈取得原価〉,〈減価償却率〉,〈期間〉)
機能
指定した期間経過したときの減価償却費の金額を求めます。
DAMTは以下の式を用いて求めます。
〈取得原価〉*〈減価償却率〉*EXP(LN(1-〈減価償却率〉)*(〈期間〉-1))
※ EXP はeの累乗、LN は自然対数
例
1,000,000円の機器を減価償却率を12%として、5年後の減価償却費を求めます。
DAMT(1000000,12%,5) → 71963.4432
数値 DDB (〈取得原価〉,〈残存価額〉,〈耐用年数〉,〈期間〉)
機能
指定した期間について、固定資産の原価償却額を倍率償却法で求めます。
〈取得原価〉は資産の取得原価を指定します。
〈耐用年数〉〈期間〉は年数を指定します。〈耐用年数〉≧〈期間〉でなければなりません。
〈取得原価〉か〈耐用年数〉か〈期間〉が0のとき、または〈耐用年数〉≧〈期間〉でないときは“#NUM#”エラーとなります。
DDBは、〈取得原価〉*2/〈耐用年数〉の式を用いて求めます。
例
新しいOA機器を300,000円で購入し、耐用年数を10年、そのときの残存価値を50,000円としたとき5年目の原価償却額は次のようになります。
DDB(300000,50000,10,5) → 24576
数値 FV (〈積立額〉,〈利率〉,〈期間〉[,〈期末/期首〉])
機能
積立額を指定期間積み立てたときの満期額を求めます。
〈利率〉と〈期間〉の単位は同じにします(利率が年利なら、期間は年数とする)。
〈期末/期首〉は、期末積立なら0、期首積立なら1を指定します。〈期末/期首〉を省略すると期末が指定されたものとします。
FVは以下の式を用いて求めます。
期首積立 〈積立額〉*((((1+〈利率〉)^〈期間〉)-1)/〈利率〉)*(1+〈利率〉)
期末積立 〈積立額〉*((((1+〈利率〉)^〈期間〉)-1)/〈利率〉)
例
毎年 100,000円ずつ年利4.9%で5年間積み立てたときの満期額は以下のようになります。
期首積立 FV(100000,4.9%,5,1) → 578481.961
期末積立 FV(100000,4.9%,5,0) → 551460.401
数値 GRATE (〈セル範囲〉)
機能
〈セル範囲〉のデータを直線で近似し、その成長率を求めます。
〈セル範囲〉のデータは左から右に、そして上から下の順に評価します。そのデータがY座標値となり、X座標値はデータの順に1,2,3... と割り当てられます。
〈セル範囲〉内の数値以外のデータ、および空セルは無視します。
例
GRATE([1,1:2,3]) → 0.26857(下図の例の場合)

数値 IRR (〈推定利益率〉,〈セル範囲〉)
機能
投資によって生じるキャッシュフローから内部利益率を求めます。
内部利益率とは投資額とそれから発生する収益額に基づく投資効率を表す利率のことです。
〈セル範囲〉にはキャッシュフローのデータを入力した範囲を指定します。〈セル範囲〉のデータは左から右に、そして上から下の順に評価します。
〈セル範囲〉で指定されたキャッシュフローの最初のデータは初期投下資本を負の数値で記入しておきます。
〈セル範囲〉内の数値以外のデータ、および空セルは無視します。
〈推定利益率〉を初期値とする近似計算をし、内部利益率が0.0000001以内の誤差で得られないときは“#NUM#”エラーとなります。
例
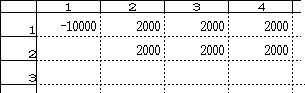
IRR(0.05,[1,1:2,4]) → 0.05471792(下図の例の場合)
数値 NPV (〈利率〉,〈セル範囲〉)
機能
想定したキャッシュフローの現価換算額を求めます。
〈セル範囲〉にはキャッシュフローのデータを入力した範囲を指定します。〈セル範囲〉のデータは左から右に、そして上から下の順に評価します。
〈セル範囲〉内の数値以外のデータ、および空セルは無視します。
NPVは以下の式を用いて求めます。
Σ〈キャッシュフローのデータ〉/(1+〈利率〉)^〈期の番号〉
※ Σは上の計算式のキャッシュフローのデータ数(期の数)分の合計を表す。
例
NPV(5%, [1,1:2,3]) → 12544.98(下図の例の場合)
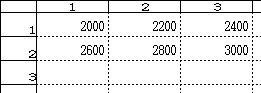
数値 PMT (〈借入額〉,〈利率〉,〈期間〉[,〈期末/期首〉])
機能
ローンの借入額を均等返済する場合の、返済額を求めます。
〈利率〉と〈期間〉の単位は同じにします(利率が年利率なら、期間は年数とします)。
年利率が12%で3年間の毎月返済なら、〈利率〉は12%/12、〈期間〉は3*12とします。
〈期末/期首〉は、期末返済なら0、期首返済なら1を指定します。
〈期末/期首〉を省略すると期末が指定されたものとみなされます。
PMTは以下の式を用いて計算します。
期末返済 〈借入額〉*〈利率〉/(1-(〈利率〉+1)^-〈期間〉)
期首返済 (〈借入額〉*〈利率〉/(1-(〈利率〉+1)^-〈期間〉))/(1+〈利率〉)
例
1,000,000円を年利3.9%で2年間で返却する場合、毎月の返済額は以下のようになります。
期末返済 PMT(1000000,3.9%/12,24,0) → 43380.427
期首返済 PMT(1000000,3.9%/12,24,1) → 43239.897
数値 PRO (〈数値〉,〈セル範囲〉)
機能
〈セル範囲〉のデータを直線で近似し、その成長率から〈数値〉(X座標)で指定した位置に出現するデータ(Y座標)を予測します。
〈セル範囲〉のデータは左から右に、そして上から下に評価します。そのデータをY座標値とし、X座標値はデータの順に1、2、3...と割り当てます。
〈セル範囲〉内の数値以外のデータ、および空セルは無視します。
例
PRO(7,[1,1:2,3]) → 2.60667(下図の例の場合)

数値 PV (〈投資額〉,〈利率〉,〈期間〉[,〈期末/期首〉])
機能
投資の現在価値を求めます。
〈期末/期首〉は、期末払いなら0、期首払いなら1を指定します。
〈期末/期首〉を省略すると期末が指定されたものとみなします。
PVは以下の式で求めます。
期末払い 〈投資額〉*(1-(〈利率〉+1)^-〈期間〉)/〈利率〉
期首払い 〈投資額〉*(1-(〈利率〉+1)^-〈期間〉)*(1+〈利率〉)/〈利率〉
例
50,000円を年利13%で5年間毎年投資した場合の現在価値を求めます。
期末払い PV(50000,13%,5,0) → 175861.563
期首払い PV(50000,13%,5,1) → 198723.566
数値 RATE (〈定期支払額〉,〈現在価値〉,〈期間〉)
機能
複利計算で、一定期間の利率を求めます。
〈定期支払額〉と〈期間〉の単位は同じにします(求める利率をひと月の利率としたいときは、ひと月の定期支払額と月数の期間で指定します)。
〈定期支払額〉〈現在価値〉〈期間〉のいずれかが0であると“#NUM#”エラーとなります。
RATEは以下の式で求めます。
EXP(LN(〈定期支払額〉/〈現在価値〉)*(1/〈期間〉))-1
※ EXPはeの累乗、LNは自然対数
例
1,000,000円を1年複利で運用するとき、5年で1,500,000円になるために必要な利率を求めます。
RATE(1500000,1000000,5) →0.08447
数値 SLN (〈取得原価〉,〈残存価額〉,〈耐用年数〉)
機能
定額法を用いて、固定資産の、期ごとの償却価額を求めます。
SLNは以下の式を用いて求めます。
(〈取得原価〉-〈残存価額〉)/〈耐用年数〉
例
新しいOA機器を300,000円で購入し、耐用年数を10年、そのときの残存価値を50,000円としたとき、毎年の原価償却額を求めます。
SLN(300000,50000,10) → 25000
数値 SYD (〈取得原価〉,〈残存価額〉,〈耐用年数〉,〈使用年数〉)
機能
指定した使用年数の年度における、固定資産の償却価額を級数法で求めます。
SYDは以下の式で求めます。
(〈取得原価〉-〈残存価額〉)*(〈耐用年数〉-〈使用年数〉+1)/(〈耐用年数〉*(〈耐用年数〉+1)/2)
例
新しいOA機器を 300,000円で購入し、耐用年数を10年、そのときの残存価値を50,000円としたとき、5年目の償却額を求めます。
SYD(300000,50000,10,5) → 27272.727
数値 TERM (〈積立額〉,〈利率〉,〈目標満期額〉[,〈期末/期首〉])
機能
目標満期額になるまでの、積立額の積み立て期間数を求めます。
〈期末/期首〉は、期末払いなら0、期首払いなら1を指定します。
〈期末/期首〉を省略すると期末が指定されたものとみなします。
TERMは以下の式を用いて計算します。
期末積立 LN(1+(〈目標満期額〉*〈利率〉/〈積立額〉))/LN(1+〈利率〉)
期首積立 LN(1+((〈目標満期額〉/(1+〈利率〉))*〈利率〉/〈積立額〉))/LN(1+〈利率〉)
※ LN は自然対数
例
年利8.9%で毎年200,000円ずつ積み立た場合に、2,000,000円になるまでの期間を求めます。
期末積立 TERM(200000,8.9%/12,2000000,0) → 9.682
期首積立 TERM(200000,8.9%/12,2000000,1) → 9.613